Modern Architectures in CNN - ResNet
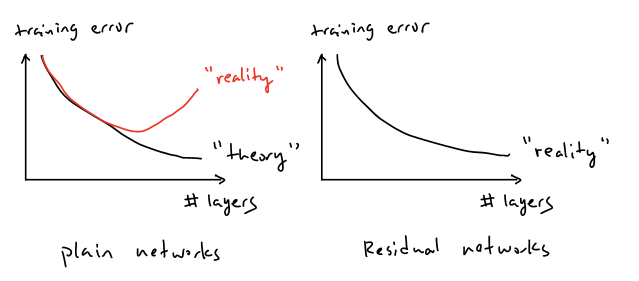
In this post, we mainly focus on one of the modern architectures, ResNet, that are commonly used nowadays and have much powerful abilities so as to achieve higher accuracy for the tasks such as classification and etc. Theoretically, in convolutional neural networks, the training error or accuracy is supposed to decrease and converge as the number of layers in CNN increases; however, before the introduction of ResNet, the researchers found out that as the number of convolutional layers increases, the training error does decrease but would bounce back and increase again if the number of layers increases significantly to some certain amounts. This phenomena is the so-called degradation problem. The figure below demonstrates the relationship between the training error and the number of layers in CNN in terms of “plain” networks and residual networks.
Residual Blocks
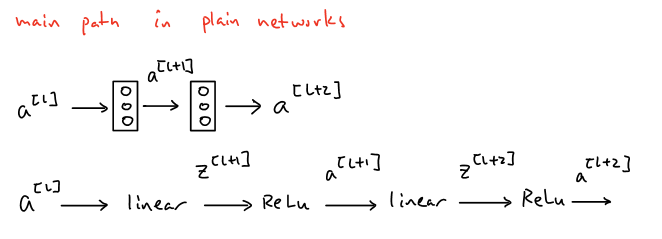
Fortunately, the innovation of ResNet helps us cope with this intractable problem and the key components of ResNet is the design of residual blocks. Before diving into details, let’s compare the differences between residual blocks in residual networks and the “plain” networks without residual blocks first. In the two-convolutional-layer “plain” networks shown below, the main path from input \(a^{[l]}\) to \(a^{[l+2]}\) is that input \(a^{[l]}\) experiences linear operations (convolutional layer) first to obtain \(z^{[l+1]}\) and goes through the ReLU activation function afterwards to generate the first-layer output \(a^{[l+1]}\), then applies another linear operation (convolutional layer) in terms of \(a^{[l+1]}\) to obtain \(z^{[l+2]}\) and goes through the ReLU activation function again to generate the final output \(a^{[l+2]}\).
The formula described above can be summarized as:
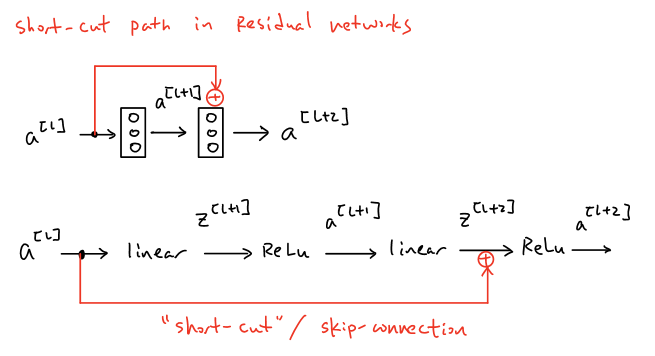
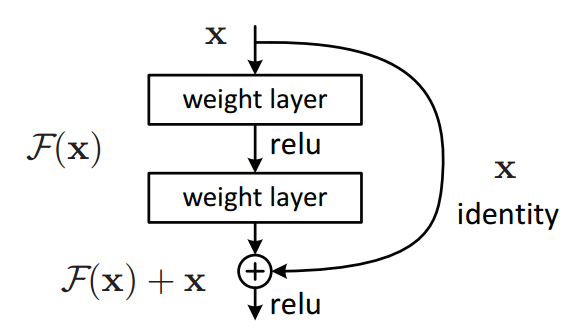
\[z^{[l+1]}=W^{[l+1]}a^{[l]}+b^{[l+1]}\\ a^{[l+1]}=g(z^{[l+1]})\\ z^{[l+2]}=W^{[l+2]}a^{[l+1]}+b^{[l+2]}\\ a^{[l+2]}=g(z^{[l+2]})\]What residual block does is that instead of choosing the main path described above in “plain” networks, residual blocks choose to go through a short-cut path, which is also called skip-connection that the network fast-forward/skip from the input to right before the second ReLU activation function. The intuition behind it is that since “plain” networks does not work well in deeper networks, we could decide to skip some extra layers in order to achieve better results. In other word, residual blocks learn residual/identity function with reference to the block input by relying on skip connections only. Because of that, the formula for one residual block becomes as followed:
The term of \(a^{[l]}\) in the forth formula makes the network to a residual network. The authors of ResNet found that by using the residual blocks in network allows us to train much deeper networks and also achieve better results as well. Why does it call residual? Consider a neural network block whose input is \(x\) and a “plain” network is actually learning the true distribution \(H(x)\), which is just the layers’ output given the input \(x\). Denote the difference/residual between output \(H(x)\) and input \(x\) as \(R(x)\). That is, \(R(x)=output-input=H(x)-x\). Consequently, the residual blocks are actually trying to learn the residual function, \(R(x)\) instead of true output \(H(x)\). And the researchers found out that it was much easier to learn the residual function between output and input rather than only the input.
Why residual blocks work?
Residual Network
The way how residual networks work is to stack every residual block shown above and integrate them together. When trianing ResNet, we either train the layers in residual blocks or skip training for those layers using skip connections. In this way, it enables us to train much deeper networks. In other words, we can skip the training of few layers using skip-connections or residual blocks.