Padding in Convolutional Neural Networks

To build a deep neural network, we need to be familiar with the basic convolutional operations such as padding, strides, pooling and etc.

In convolutional neural network, a convolutional layer is applied to one or more filters to an input in order to generate output. The input is typically 3-dimensional images (height, width, channels) while the filters are also 3-dimensional shape with the same number of channels and different heights and widths. For example, suppose the input size is \(n\times n\times c\), then the filters are commonly with the shape of i.e. \(3\times 3\times c\) or \(5\times 5\times c\). As such, the filters are repeatedly applied to each part of the input image, resulting in a feature map.

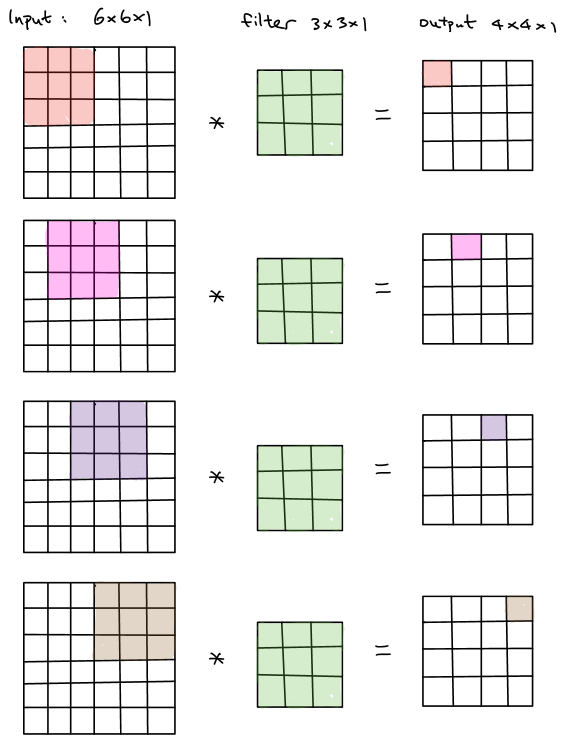
For instance, we want to convolve a \(6 \times 6\times 1\) image input with a \(3\times 3\times 1\) filter. The resulting output will be \(4 \times 4\times 1\), which is illustrated below.

In general, a \(n \times n\times c\) input convolved with a \(f \times f\times c\) filter will generate a \((n-f+1) \times (n-f+1) \times 1\) output. In order word, the shape of output shrinks every time when convolutional operations are completed. It will result in a relatively small output shape without any padding, which is the problem that we want to avoid since once the convolutional neural network goes deeper, the output of each layer becomes smaller and smaller. On the other hand, the corner pixels of the image convolve much less times than the others. It throws away a lot of information near the edge of the input.

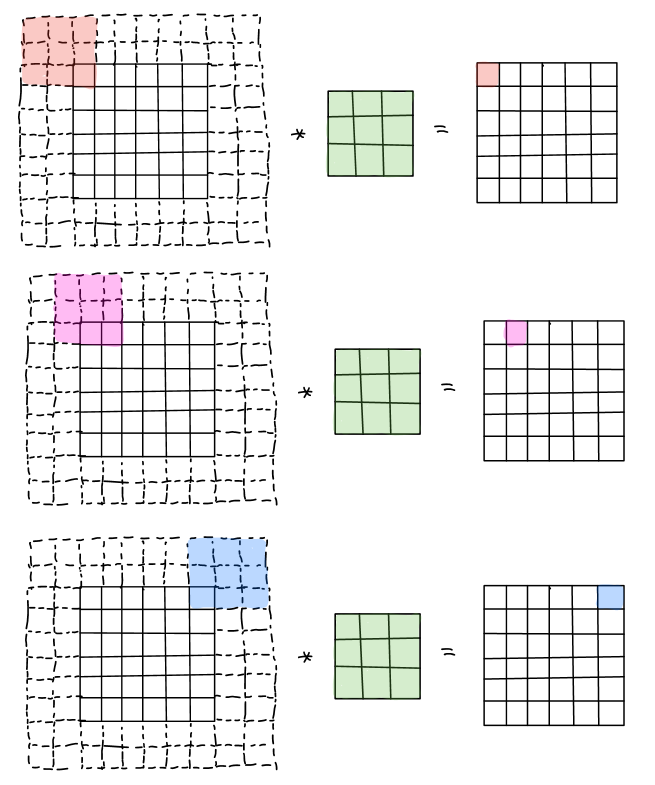
To solve both of the problems aforementioned, we typically apply padding. In this case, by adding one pixel with intensity value of zero in each border of the input, that is \(p=1\), the shape of the padded input becomes \(8\times 8 \times 1\). By convolving with a \(3\times 3\times 1\) filter, instead, the generated output is \(6\times6\times1\), which is the same size as the original input. By doing that, we could successfully avoid the problems.

Valid and Same convolutions

There are two common convolution types: valid and same convolutions.

For valid convolution, it refers to no padding (\(p=0\)). That is, for a \(n\times n\times c\) input that convolves with a \(f\times f\times c\) filter, the generated output size will be \((n-f+1)\times (n-f+1)\times 1\).

For same convolution, it refers to padding so that output size is the same as the input size, which is commonly used in convolutional neural networks. By padding with \(p\) pixels in each border, the padded input size becomes \((n+2p) \times (n+2p) \times c\). After convolving with a \(f\times f\times c\) filter, the output size should be \((n+2p-f+1) \times (n+2p-f+1) \times 1\). Since it is a same convolution, then output size should be equal to the unpadded input size, that is \(n+2p-f+1=n\), which is \(p=\frac{f-1}{2}\). Thus, in the case of same convolution, the value of padding is only impacted by the size of the filter and vice versa. By convention, the size of filter is always odd instead of even.

Stride convolution

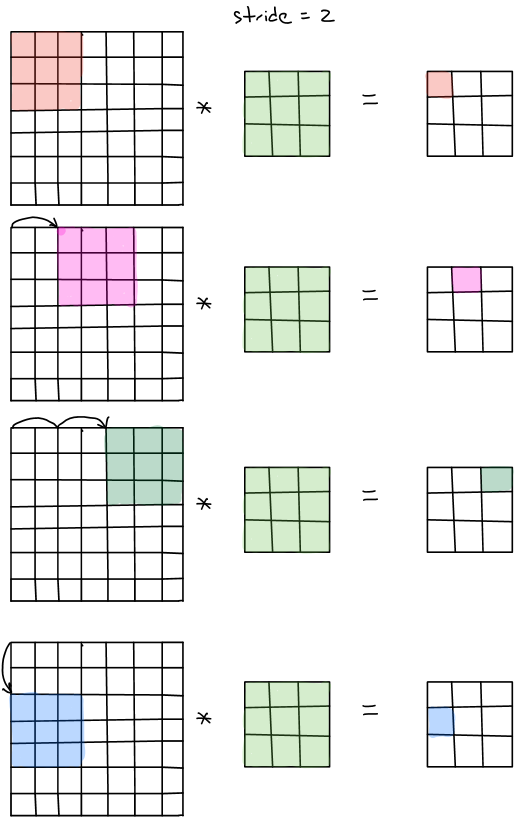
Stride convolution is another basic building blocks in convolutional neural networks. Let’s take an example of convolving \(7\times7\times1\) input with a \(3\times3\times1\) filter with the stride of 2.

The procedures are illustrated below.

In summary, to convolve a \(n\times n\times c\) with a \(f\times f\times c\) filter with the stride \(s\) and padding \(p\), the generated output size should be \((\frac{n+2p-f}{s}+1) \times (\frac{n+2p-f}{s}+1) \times 1\). However, in some cases, the value of \(\frac{n+2p-f}{s}\) sometimes is not integer, thus we will take the floor value, which is \(\lfloor \frac{n+2p-f}{s} \rfloor\).