Activation Function

As mentioned before, each layer except the output layer usually has an activation function, i.e. \(a^{[1]}=\sigma(z^{[1]})\) represents the first hidden layer uses sigmoid function as activation function. There are several common activation function that are used in deep learning, which are sigmoid, tanh, ReLU and leaky ReLU activation functions.

Now let’s see how those functions works and why it is necessary to have activation function in neural networks.

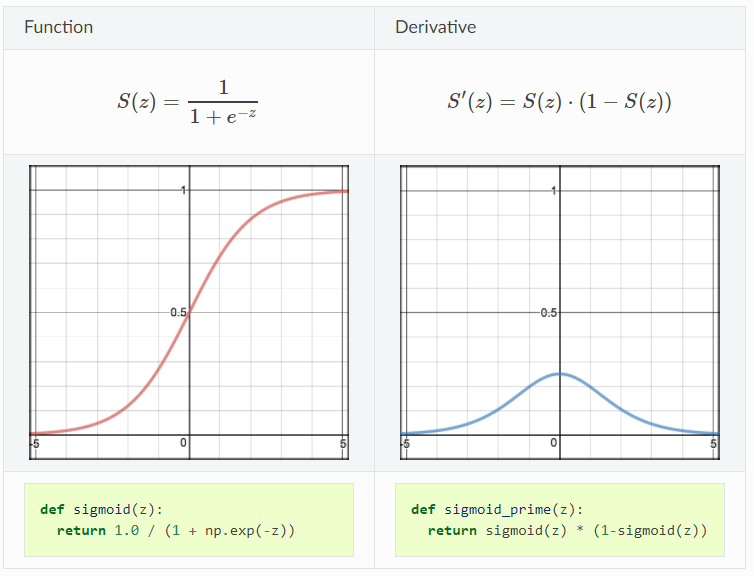
Sigmoid

Sigmoid activation function takes a real value as input and outputs another value between 0 and 1, which has been introduced in the past posts. It has all the nice properties of activation function: non-linear, continuously differentiable, monotonic and has a fixed output range. One thing needed to be noticed is the reason why we want the activation function to be non-linear. It is because if the activation function is linear, then its derivative will be always constant when conducting gradient descent method, which implies that the algorithm is not learning any useful parameter at all. The demonstration of sigmoid function and its derivative are shown below:

Pros:

• nonlinear
• smooth gradient
• good for classification
• have the activation bound in a range of (-1,1)

Cons:

• the Y values tend to respond very less to changes in X toward both ends of the activation function
• it gives rise to a problem of “vanishing gradients”
• the output isn’t zero-centered and it makes the gradient updates go too far in different direction
• sigmoid saturates and kills gradient.

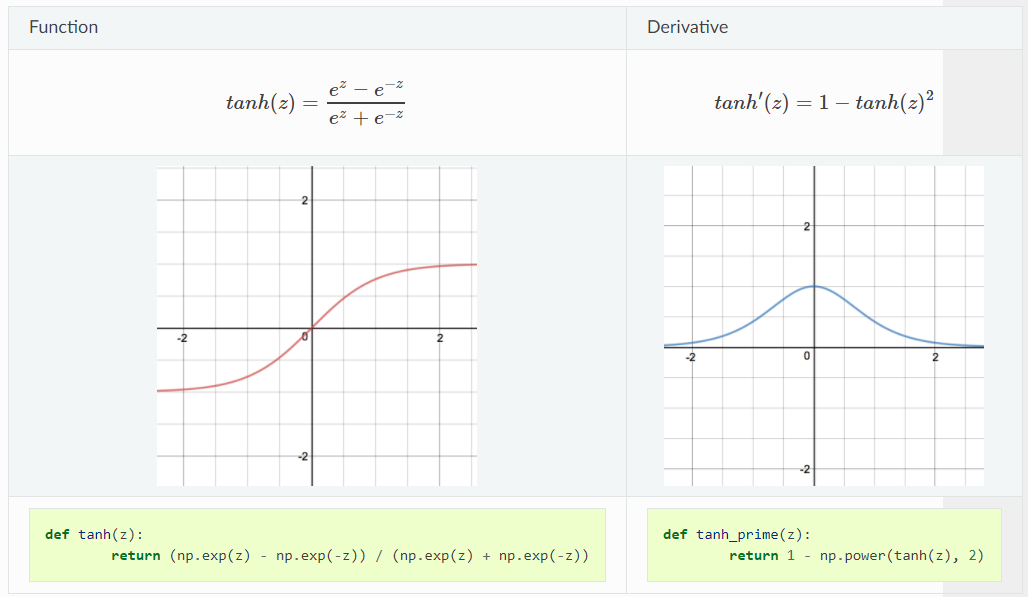
Tanh

Like sigmoid activation function, tanh function is also non-linear with similar demonstration of shape except that tanh activation function is zero-centered, which makes it popular and widely used activation function. The demonstration of tanh function and its derivative are shown below:

\[tanh(x)=\dfrac{2}{1-e^{-2x}}-1\]

Pros:

• the gradient is stronger for tanh than sigmoid since the derivatives are deeper.

Cons:

• similar to sigmoid, tanh activation function also has the problem of vanishing gradients

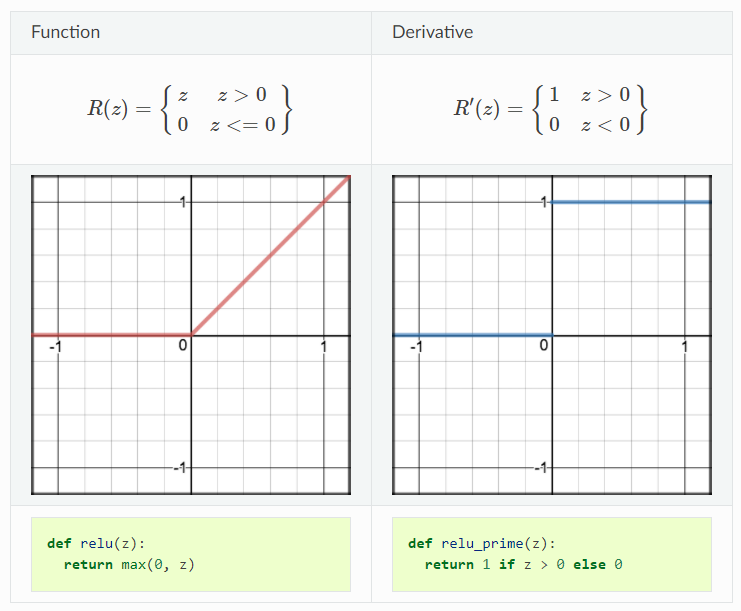
ReLU

ReLU is another nonlinear activation function but not bounded. The range of ReLU is from 0 to infinity, which infers that it can blow up the activation. ReLU gives the benefit of sparsity and efficiency. Imagine a huge neural network and we would ideally make a few neurons in the network not activate and thereby making the activation sparse by using ReLU activation function because of its zero value of output in terms of the negative input. In that way, the networks would become much less costly and it enables us to deal with much deeper networks. The demonstration of ReLU function and its derivative are shown below:

However, there is also a problem called dying ReLU problem due to that region in activation function (when input is negative) since gradient will be 0 in that region and thus the weights will not be adjusted during gradient descent. That means, those neurons that go into negative state will stop responding to variations in error/input which cause those neurons to die and not respond making a substantial part of the network passive. To solve this type of problem, people sometimes use leaky ReLu where the negative region becomes a slightly inclined line rather than horizontal line, which will be addressed below.

Pros:

• nonlinear
• avoid vanishing gradient problem
• less computationally expensive than tanh and sigmoid

Cons:

• some gradients can be fragile during training and can die.
• ReLU problem
• it can blow up the activation due to the range of output (0, inf)

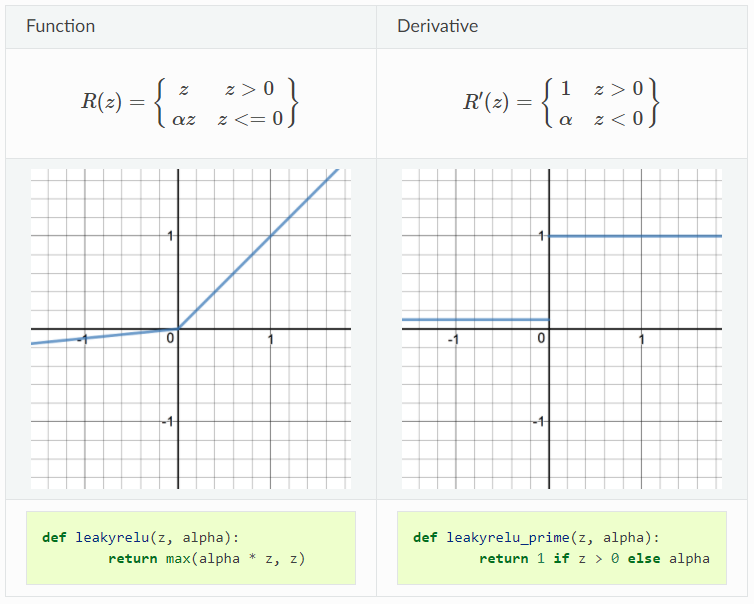
Leaky ReLU

Leaky ReLU is a variant of ReLU, instead of being 0 when input is negative, leaky ReLU allows a small, non-zero and constant gradient \(\alpha\) (\(\alpha=0.01\) usually). However, the consistency of the benefit across tasks is presently unclear. The demonstration of ReLU function and its derivative are shown below:

Pros:

• leaky ReLU is one attempt that somehow fixs the “dying ReLU” problem by having a small negative slope when input is negative

Cons:

• As it possess linearity, it can’t be used for the complex Classification. It lags behind the Sigmoid and Tanh for some of the use cases.

Why activation functions?